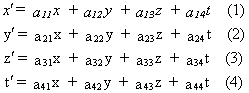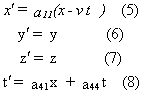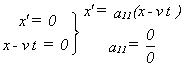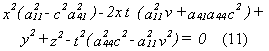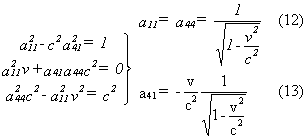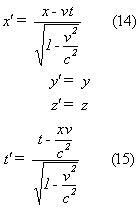|
Proof of the Falsity of the Theory of Relativity |
|
An example of a popular, but faulty derivation of the Lorentz or transformation equations, followed by a philosophical proof of the falsity of the special theory of relativity (and with it the general theory of relativity).
© Erik J. Lange 1999-2024
Last revision: 11-12-2006 (dd-mm-yyyy), abstract added on: 08-02-2023 |
|
Abstract
Einstein’s special and general relativity theory are intrinsically wrong and they cannot be repaired. The essence of what’s wrong with relativity theory is that there does not and cannot exist a physical paradigm (in particular some definition of time and space) in which one random velocity (the speed of light in this case) is absolute while all other velocities are relative.
In all derivations of the relativistic Lorentz transformation equations a relative velocity “v” (this is the
velocity between the two reference frames used in the derivation) and the speed of light “c” appear, the latter
of which is assumed to be absolute (“absolute” here meaning that an observer would always measure the same
speed of light, regardless of his own state of linear motion). To have a relative and an absolute velocity in
the same derivation is an impossibility because they represent two different, clashing physical paradigms. The
existence of a single relative velocity in one’s world view actually means agreeing that all velocities are
relative because you assume an absolute time and absolute space (as far as those are “definitions” of time and
space): exactly that makes all velocities relative, no exceptions possible.
Note that the possibility of an absolute frame of reference for the propagation of light is irrelevant to this discussion since it has no consequences for our choice of paradigm as far as the absoluteness of time and space are concerned. Short introduction
Today (1999) the theory of relativity by Albert Einstein is still a generally accepted theory. Although there have been raised a number of objections against the theory since its first publication in 1905, none of these have been able to convince the scientific community of the falsity of the theory. On philosophical, mathematical and empirical grounds, there are nevertheless many valid objections against the theory to be found. This article focuses on two of these, in an analysis of a popular derivation of the Lorentz transformation according to the theory of special relativity and by means of a philosophical argument showing a contradiction between the two postulates of special relativity.
The purpose of Einstein's theory was to create a system of equations which would describe the transformation of coordinates from one reference frame to another. Hereby the two reference frames have a relative velocity v with respect to each other, and the coordinates to be transformed, describe the movement of the front of a light signal which is supposed to have a velocity c with respect to all uniformly moving reference frames.
The general opinion at the time was that one could conclude from experiments, that light (in vacuum) would always have the same (measured) constant velocity, irrespective of the velocity of the observer. Because this was in contradiction with classical relativity according to Newton, there had to be thought up a new theory which would unite classical relativity with the constancy of the speed of light. This resulted in special relativity theory.
Analysis 1
Einstein based his special theory of relativity on two postulates: 1. The laws of physics are the same in all inertial systems (reference frames that move uniformly and without rotation). There are no preferred inertial systems. When a certain reference frame moves with constant speed with respect to another, processes of nature will obey the same laws of physics in either reference frame. 2. The speed of light in vacuum has the same constant value c in all inertial systems.
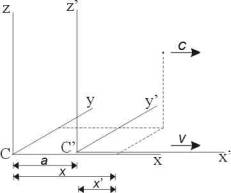
The two postulates can be translated to mathematics by using a schematic situation in which there are two reference frames which have a uniform motion with respect to each other (see the figure). If the second postulate is true, observers in both reference frames will measure the same speed of light.
Simplified, the speed of light can be written as the covered distance x of a light signal, divided by the transit time t. With respect to a reference frame C a light signal propagates along the x-axis in positive direction, according to: x = ct (where c equals 300.000 km/sec) The same light signal travels, according to Einstein, also with respect to reference frame C' with a speed equal to c. With respect to C', the equation for the movement of the light signal then becomes x'=ct'.
The velocity v of frame C' with respect to frame C, can be calculated by dividing the covered distance along its x-axis by the transit time. Because of symmetry, v can be observed equally from within C and C'. Do note that, from within C, at any point in time (coordinate) t>0, the coordinate x of the origin of C' will be smaller than the coordinate x of the front of the light signal. To the entire derivation discussed in this article, it applies that C' coincides with C at coordinates t=0 and t'=0. The coordinates x and x' of the front of the light signal are at that very moment also equal to zero.
Because of his second postulate, Einstein had to make concessions in relation to both the spatial properties of moving objects (in the form of a length-contraction), as well as to the concept of absolute time as it was generally conceived back then (resulting in a time-dilation in the moving reference frame).
________________________
The following derivation of the Lorentz transformation according to the special theory of relativity, is a version of the derivation of the transformation equations that can be found frequently in the literature1, 2. This version is taught on universities around the world.
The light signal (in figure above) moves uniformly rectilinear with respect to both reference frames. So we need to transform a uniformly rectilinear motion in C into another in C'. This means there must be a linear relation between coordinates x, y, z, t and x', y', z', t'. The most common form of this relation, as needed by, and according to the special theory of relativity, is as follows:
Note that the inclusion of the coordinates t and t' is specific to relativity theory: this is necessary if one hopes to find a transformation equation between them.
Because C' moves linearly along the x-axis of C, it always applies that y=y' and z=z'. From this follows for the coefficients:
Because of symmetry, t' can only depend on x and t. From this follows:
Then it is assumed that x'=0 in C' has to correspond with x=vt in C. It follows for the coefficients that:
When the coefficients in equations (1), (2), (3) and (4) are substituted by their values we get:
The falsity in this derivation can be located in the assumption that x'=0 has to correspond with x=vt. The equations (1) up to and including (4) are the most general form of a linear transformation of four-dimensional space-time coordinates, of an event that is - events have a location in space, dependent on a time coordinate. At that point in the derivation this event is the observation from within C and from within C' of the spatial coordinates of any phenomenon (not necessarily the front of a light signal yet) in uniform, rectilinear motion, at a certain point in time which may be different to both observers. We should not interpret x'=0 as being the origin of C', the reference frame itself, because when observed from within C' it is not an event in the intended sense: this x' is independent of time. Any assumed coordinate must relate to a proper event. Therefore
x'=0 for x=vt must apply to an event just coinciding with the origin of C', and
is not a part of the reference frame C' itself. But only of the origins of the reference frames
themselves we know for sure that the distance between them is vt: we do not know if the coordinate x of said proper event as observed from within C can transform to x'=0 as observed from within C', for an observed t coordinate (>0) relating to x according to x/t=v. After all, the derivation of the Lorentz equations is meant to be able to determine such a
transformation in the end: we cannot assume it at the start.
The only correct, but useless, way I can see to bring v into play, is by deducing: x=vt+x'C. (Note the important subscript C in x'C.) This variable x'C represents the travelled distance of the uniformly, rectilinear moving phenomenon in C', as observed from within C. This will be different from the coordinate x' in equation (1) which must result from observation from within C'. As mentioned, this correction won't help the derivation of the transformation equations at all. The problem is that we can't make any one of the coordinates zero, without making them all zero. Note that the relativistic transformation of space-time coordinates is a transformation from one observation system into another. Therefore, all primed coordinates in this derivation are to be observed from within C'; the primed coordinates as observed from within C are subject to classical transformation and should be trivial here.
The mistake which was being made in the assumption that led to equations (5), (6), (7) and (8) does indeed show up in those equations. Specifically in equation (5) an error can be found, for in equation (5) a11 can’t be solved (as is intended later on):
For the sake of completeness, the rest of the derivation will be shown in short.
When a light signal is transmitted in arbitrary direction at coordinates t=t'=0, then the covered distance of the signal with respect to C can be determined with Pythagoras and satisfies therefore:
With respect to C' applies (according to the second postulate):
Substitution of equations (5), (6), (7) and (8) in equation (10) gives:
Equation of (9) and (11) leads to the next three equations for determining a11, a41 and a44:
In deriving (12) and (13), the signs (- or +) are chosen so that when v becomes equal to zero (!), the equations (5), (6), (7) and (8) change into:
Substitution of equations (12) and (13) in (5), (6), (7) and (8) gives the Lorentz transformation:
(H.A.Lorentz derived equations (14) and (15) first, based on an ether theory, years before Einstein first published his special relativity theory.)
Note
again that these equations describe the transformation of two coordinates
x and t (as observed from within C) into x' and t' (as observed from
within C') of the front of a light signal, where x/t=c and x'/t'=c
according to special relativity.
The error leading to the falsity of this derivation also appears in Einstein's other derivations of the transformation equations (in his original article3 and much later in another and “simplified” form in his book about relativity4 ). But the falsity of these derivations does not prove of course that in principle a good derivation can’t be made at all. A proof of this sort lies more on a philosophical and empirical plane I think. I consider, for instance, the postulate of the constant speed of light to be in contradiction with Galilean transformation and therefore false: the relativity of speeds in general makes one absolute speed impossible. Furthermore and perhaps foremost, I think the Kennedy-Thorndike experiment5 (an altered version of the famous Michelson-Morley experiment) shows that the relativistic transformation equations can never explain nor describe the results thereof. (The Kennedy-Thorndike experiment implies that for each conceivable difference in length between the arms of an interferometer, a different length contraction factor should apply.) See analysis 2 below for a proof based on a contradiction between the two postulates of special relativity theory.
Analysis 2
To proof relativity theory wrong it is not enough to show the errors in the several existing mathematical derivations of the transformation equations, since it might always be possible to derive a new one in the future. So probably we have to focus more on non-mathematical, experimental and philosophical arguments (as mentioned above) to falsify relativity. This is especially hard because almost any observation or experiment concerning the propagation of light has apparently been explained within relativity theory and because argumentative reasoning quickly results in vagueness and endless discussions. Now, proving explanations for experiments wrong can only be the last step in the process of falsifying a theory, I think, since to be convincing at this, agreement is required about the principles of the theory, the behavior of what is measured, the justness of the method of measuring, and the interpretation of the measurements. So I'll first have to attempt to make a logical argument anyway. Other attempted proofs of the falsity of special relativity theory often founder on confusion about the relativistic effects of time-dilation and length-contraction. The question of whether these effects are real or only observational, and thus relative (subjective), and how the nature of these effects relates to the moving reference frames and their physical reality are at the heart of the problem of dealing with relativity. Therefore, the following text will try to clear up this issue for once and for all.
As we know, Einstein based his special theory of relativity on the following two postulates: 1. The laws of physics are the same in all inertial systems (reference frames that move uniformly and without rotation). There are no preferred inertial systems. When a certain reference-frame moves with constant speed with respect to another, processes of nature will obey the same laws of physics in either reference-frame. 2. The speed of light in vacuum has the same constant value c in all inertial systems.
In relativity, time is a matter of clocks. A clock which is in rest with respect to one's own inertial system will run correctly and at a "normal" pace. This last statement is true in classical physics as well as in relativity theory. Whatever clock we use, its working is based on some natural process, which is assumed to repeat itself evenly and therefore mark even "lengths of time". According to Einstein's first postulate these processes of nature will obey the same laws of physics in all inertial frames. So clocks behave in the same way in all inertial frames, irrespective of the relative (uniform) motion those frames have with respect to each other. The first undisputable conclusion based on the first postulate and on logic reasoning is therefore: 3. Relativistic time-dilation is never a real physical phenomenon, that is to say: in the inertial system of a clock, the clock always runs normal, and behaves the same as it would in any other reference system. Measuring the time it takes any physical process to complete within the inertial system of the clock, will in all inertial frames yield the same results using said clock in the same system as in which the process takes place.
Length-contraction in relativity is something that applies to moving physical objects of practicably measurable lengths. The idea came out of an ether theory in which the earth (and all objects on it) was thought to get contracted in length in the direction of its motion around the sun, whilst moving through a medium for light-waves (which was supposed to be at rest with respect to the sun). In this theory there clearly existed a physical cause for a possible contraction. However, when with the advent of relativity theory the notion of the ether was discarded, the physical possibility of a contraction was also taken away. Since the first postulate states that there is no preferred inertial system, an object must have the same spatial properties in all inertial systems, regardless of its speed with respect to other inertial frames. In other words: a real length-contraction would have to be correlated to one particular speed, but since any inertial frame has an infinite number of (relative) velocities (depending on the inertial frame from which this velocity is measured, because of the lack of a preferred inertial system), a real length-contraction is impossible: 4. Relativistic length-contraction is never a real physical phenomenon. Spatial properties of any object are constant within its own inertial frame of reference, and are not physically altered due to any velocity this frame might have with respect to another.
From 3 and 4 we can induce: 5. All basic relativistic effects (time-dilation and length-contraction) can, if observed, only be of relative or subjective nature, due to observational circumstances, as in the observation of a natural process from within another inertial frame than the one in which said process takes place, or because of the limited speed of information transfer in the observation.
So, when discussing thought-experiments, real experiments or observed phenomena within relativity theory, conclusions 3, 4 and 5 should always apply as should the postulates of course. With this in mind (at least when agreement on these conclusions has been reached) it suddenly becomes much easier to discuss empirical and thought-experiments.
Now, assuming that in principle it is possible to directly (!) measure space-time coordinates of the front of a light signal, we can deduce from the relativistic transformation equations that the value of the x' coordinate (as observed from within C') will always (for t>0 and 0<v<c) be in between ct and 0 (with x=ct), but greater than the result of the Galilean transformation ct-vt. Note that the greater value of x' is indeed a consequence of contraction. This is because length-contraction only applies to physical objects such as rulers, not to the space in which light travels. So as the ruler contracts, the measurement of the location of the front of the signal will increase. For all physical objects however, no length-contraction will manifest itself to the observer in C', since all objects are contracted by the same factor as the rulers are. The
value of the t'
coordinate (as observed from within C') will always (for t>0 and 0<v<c) be
in between t and 0, while in classical physics time is absolute so that t'
is always equal to t. Just the fact that these coordinates differ from what would be expected from Galilean transformations (which in relativity do still apply to the calculation of the primed coordinates observed from within C) demonstrates that the second postulate (which is the sole foundation of the relativistic transformation equations) requires the relativistic effects to be real physical phenomena. Without
real physical relativistic effects, all measuring tools in C'
would be left unchanged and the observer in C' would measure different values for x' and
t'. In other words: if you negate
the physical reality of the relativistic effects,
then from the unchanging properties of space and time in all inertial
systems it follows that the classical addition of velocities should always
apply, and that Einstein's absolute and constant speed of light is in
contradiction with that addition theorem.
For a century now, special relativity managed to achieve the impossible: to make spatial dimensions and the pace of time, derivatives of (one particular) velocity, when only the opposite can be true since velocities can't be measured directly, only calculated from measurements on time and space. A thorough review of our physical paradigm appears to be necessary.
Erik J. Lange
__________________ 1. Introduction to Special Relativity, R. Resnick, J. Wiley & sons Inc., 1968 2. Klassieke Mechanica en Relativiteitstheorie, J.J.J. Kokkedee, Uitg. T.U. Delft, 1992 3. A. Einstein, “Zur elektrodynamik bewegter Kцrper”, Annalen der Physik. IV. Folge. 17, page 891, 1905. 4. Relativiteit, speciale en algemene theorie, A. Einstein, Het Spectrum, 1978. (See also the online English version of this book: Relativity, the special and general theory.) 5. R.J. Kennedy and E.M.Thorndike, “Experimental establishment of the relativity of time”, the Physical Review, vol. 42, second series, page 400, 1932.
The following links might also be of interest: John Chappell Natural Philosophy Society
|